TEOREMA DE TALES

Teorema de Tales: importante ferramenta na determinação
de medidas utilizando a proporcionalidade

Tales de Mileto foi um importante filósofo, astrônomo e matemático grego que viveu antes de Cristo. Ele usou seus conhecimentos sobre Geometria e proporcionalidade para determinar a altura de uma pirâmide. Em seus estudos, Tales observou que os raios solares que chegavam à Terra estavam na posição inclinada e eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos, observe a ilustração:

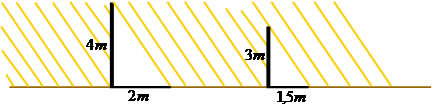
Com base nesse esquema, Tales conseguiu medir a altura de uma pirâmide com base no tamanho da sua sombra. Para tal situação ele procedeu da seguinte forma: fincou uma estaca na areia, mediu as sombras respectivas da pirâmide e da estaca em uma determinada hora do dia e estabeleceu a proporção:

O Teorema de Tales pode ser determinado pela seguinte lei de correspondência:

“Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.

Para compreender melhor o teorema observe o esquema representativo a seguir:

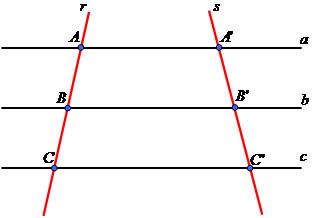
Pela proporcionalidade existente no Teorema, temos a seguinte situação:

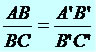
Fonte: http://www.brasilescola.com/matematica/teorema-tales.htm, acesso em 17/05/16.

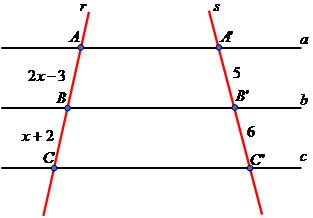
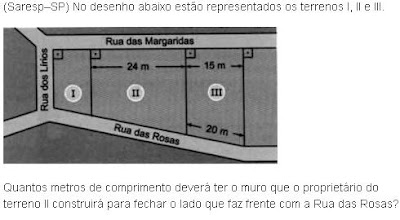
Exercício 1

Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:

Exercício 2   Qual é o valor de y?

Exercício 3